Thursday, September 29, 2011
Saturation - Non-Linear
- An ideal op amp could provide an infinite output voltage range.
- A very good op amp could provide outputs at least up to the power supply voltages.
- Most op amps fall short by about two volts so with a 12 volt supply, the output would be only ten volts.
- The output should be directly proportional to the input. That is perfectly linear.
The image below shows ideal (black line) and non-ideal (red and blue lines) behaviour including clipping when the op amp is saturated and the output voltage can go no higher.
source:http://www.softwareforeducation.com/wikileki/index.php?title=Ideal_Op-Amps
Sunday, September 25, 2011
Tuesday, September 13, 2011
Envelope Detector
The illustration shows what happens in the worst possible situation where the modulating signal is a squarewave whose frequency isn't much lower than the carrier frequency. Similar, but less severe, problems can arise with other modulating signals.
Consider what happens when we have a carrier frequency,
The above implies that we can avoid negative peak clipping by choosing a small value of
source:http://www.st-andrews.ac.uk/~jcgl/Scots_Guide/RadCom/part9/page2.html
Thursday, September 8, 2011
Friday, September 2, 2011
Wednesday, August 31, 2011
Engineering and Tech Expo
Wednesday, September 21, 2011
10 a.m. - 3 p.m.
Fargodome
The NDSU Engineering & Tech Expo is an annual event attended by employers from many engineering and technology-related industries. The expo provides an excellent opportunity to connect with students to discuss or interview for current and/or future career-related employment and co-op/internship opportunities. Last year 110 employers and 1365 students took part in this event.
The Expo is open to NDSU students and alumni and current students from Minnesota State University Moorhead Construction Management and Industrial Technology departments. The Expo is NOT open to the general public.
Individuals with disabilities are invited to request reasonable accommodations to participate in NDSU-sponsored programs and events. To request an accommodation(s), please contact the Career Center at 701-231-7111 .
Tuesday, August 30, 2011
Thursday, August 25, 2011
Friday, August 19, 2011
Volts, Amps, Ohms
Definitions:
V = Voltage (Volts)
I = Current (Amps)
R = Resistance (Ohms)
P = Power (Watts)
Analogy:
Plumbing pipes.voltage <-> water pressure
increase the pressure in the tank -> more water come out of the hose.
increase the voltage -> more current flow.
resistance <-> pipe size.
increase the diameter of the hose -> more water come out of the hose.
decrease the resistance in an electrical system -> which increases the current flow.
In either cases you increase the water flow rate or current flow
Electrical power is measured in watts.
P = VI
Take a hose and point it at a waterwheel like the ones that were used to turn grinding stones in watermills. You can increase the power generated by the waterwheel in two ways.
1) increase the pressure of the water coming out of the hose, it hits the waterwheel with a lot
more force and the wheel turns faster, generating more power.
2) If you increase the flow rate, the waterwheel turns faster because of the weight of the extra water hitting it.
Ohms Law
V=IR
I=V/R
R=V/I
Power
P=VI
Assuming DC
AC calculations introduce something called the "power factor"or Phase shift between Voltages and Currents.source:
http://www.idc-online.com/technical_references/pdfs/electrical_engineering/Volts_Amps_and_Ohms.pdf
Wednesday, April 6, 2011
Losses in a D.C. Machine
The losses in a d.c. machine (generator or motor) may be divided into three classes viz (i) copper losses (ii) iron or core losses and (iii) mechanical losses. All these losses appear as heat and thus raise the temperature of the machine. They also lower the efficiency of the machine.
1. Copper losses
These losses occur due to currents in the various windings of the machine
Note. There is also brush contact loss due to brush contact resistance (i.e., resistance between the surface of brush and surface of commutator). This loss is generally included in armature copper loss.
2. Iron or Core losses
These losses occur in the armature of a d.c. machine and are due to the rotation of armature in the magnetic field of the poles. They are of two types viz., (i) hysteresis loss (ii) eddy current loss.
(i) Hysteresis loss
Hysteresis loss occurs in the armature of the d.c. machine since any given part of the armature is subjected to magnetic field reversals as it passes under successive poles. Fig. (1.36) shows an armature rotating in two-pole machine. Consider a small piece ab of the armature. When the piece ab is under N-pole, the magnetic lines pass from a to b. Half a revolution later, the same piece of iron is under S-pole and magnetic lines pass from b to a so that magnetism in the iron is reversed. In order to reverse continuously the molecular magnets in the armature core, some amount of power has to be spent which is called hysteresis loss. It is given by Steinmetz formula. This formula is
In order to reduce this loss in a d.c. machine, armature core is made of such materials which have a low value of Steinmetz hysteresis co-efficient e.g., silicon steel.
(ii) Eddy current loss
In addition to the voltages induced in the armature conductors, there are also voltages induced in the armature core. These voltages produce circulating currents in the armature core as shown in Fig. (1.37). These are called eddy currents and power loss due to their flow is called eddy current loss. The eddy current loss appears as heat which raises the temperature of the machine and lowers its efficiency.
core resistance can be greatly increased by constructing the core of thin, roundIf a continuous solid iron core is used, the resistance to eddy current path will be small due to large cross-sectional area of the core. Consequently, the magnitude of eddy current and hence eddy current loss will be large. The magnitude of eddy current can be reduced by making core resistance as high as practical. The iron sheets called laminations [See Fig. 1.38]. The laminations are insulated from each other with a coating of varnish. The insulating coating has a high resistance, so very little current flows from one lamination to the other. Also,
because each lamination is very thin, the resistance to current flowing through the width of a lamination is also quite large. Thus laminating a core increases the core resistance which decreases the eddy current and hence the eddy current loss.
It may be noted that eddy current loss depends upon the square of lamination thickness. For this reason, lamination thickness should be kept as small as possible.
3. Mechanical losses
These losses are due to friction and windage.
(i) friction loss e.g., bearing friction, brush friction etc.
(ii) windage loss i.e., air friction of rotating armature.
These losses depend upon the speed of the machine. But for a given speed, they are practically constant.
Note. Iron losses and mechanical losses together are called stray losses.
Constant and Variable Losses
The losses in a d.c. generator (or d.c. motor) may be sub-divided into
(i)constant losses (ii) variable losses.
(i) Constant losses
Those losses in a d.c. generator which remain constant at all loads are known as
constant losses. The constant losses in a d.c. generator are:
(a) iron losses
(b) mechanical losses
(c) shunt field losses
(ii) Variable losses
Those losses in a d.c. generator which vary with load are called variable losses.
The variable losses in a d.c. generator are:
Total losses = Constant losses + Variable losses
Note. Field Cu loss is constant for shunt and compound generators.
http://electricalandelectronics.org/2009/05/07/losses-in-a-dc-machine/
Sunday, March 20, 2011
Friday, March 18, 2011
Saturday, February 12, 2011
FOR PROBLEM 12.13 DO ONLY PART (a) NMOS. PROBLEM 12.13 IS SIMILAR TO EXAMPLE PROBLEM 12.9 (uploaded)
QUIZ 3 IS ON WEDNESDAY - 02/16/2011



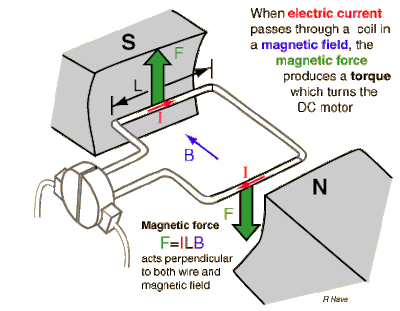
 Magnetic Field in DC Motor
Magnetic Field in DC Motor